Data Abstraction and Closures
This example is an adaptation of the SICP Picture Language example found in the book Structure and Interpretation of Computer Programs. In this exercise I will translate the original Scheme implementation to Javascript and use it as a tutorial to drive home the importance of closures, data abstraction. The complete code can be found in the picturelang.
A Picture Language
This section present a simple language for drawing pictures that illustrates the power of data abstraction and closure, and also exploits higher order procedures in an essential way.The language is designed to make it easy to experiment with patterns such as this one
which are composed of repeated elements that are shifted and scaled. In this language, the data objects being combined are represented as functions instead of objects or lists. The functions in this language satisfy the closure property. This allows us to easily build arbitrary complicated patterns.
In general an operation for combining data objects satisfies the closure property if the result of combining things with that o peration can themselves be combined using the same operation. Closure is the key to power in any means of combination because it permits us to create hierarchical structures - structures made up of parts, which themselves are made up of parts, and so on.
The picture language
Part of the elegance of this picture language is that there is only one kind of element, called a painter. A painter draws an image that is shifted and scaled to fit within a designated parallelogram-shaped frame. For example, there is a primitive painter we call Wave that makes a crude line drawing
The Javascript code to use a Wave painter and draw it onto a Frame is the follows:
var c = document.getElementById("canvas");
var ctx = c.getContext("2d");
var frame = new Frame(ctx, new Vector2(0, 0),
new Vector2(480,0),
new Vector2(0,480));
var painter = Wave();
painter(frame)
What is important to note is that the actual shape of the drawing depends on the Frame. So if we create a smaller frame (but still use the same html canvas) the Wave painter would scale accordingly.
var c = document.getElementById("canvas");
var ctx = c.getContext("2d");
var frame = new Frame(ctx, new Vector2(0, 0),
new Vector2(240,0),
new Vector2(0,240));
var painter =Wave();
painter(frame)
Painters can be more elaborate than this for example we can have a painter which paints an image retrieved from the web, for now we will stick to the simple Wave painter.
To combine images, we use various operations that construct new painters from given painters (closure!). For example Besides operation takes two painters and produces a new, compound painter that draws the first painter’s image in the left half of the frame and the second painter’s image in the right half of the frame.
Similarly, Below takes two painters and produces a compound painter that draws the first painter’s image below the second painter’s image.
Some operations transform a single painter to produce a new painter. For example FlippedVert takes a painter and produces a painter that draws its image upside-down,
and FlippedHorz produces a painter that draws the original painter’s image left-to-right reversed.
Wave4 is a painter that is build up in two stages starting from Wave.
In building up a complex image in this manner we are exploting the fact that painters are closed under the language’s means of combination. The Beside and Below of two painters is itself a painter; therefore, we can use it as an element in making more complex painters.
Once we can combine painters, we would like to be able to abstract typical patterns of combining patters. We will implement the painter operations as Javascript functions. This means that we do not need a special abstraction mechanism in the picture language. Since the means of combination are ordinary Javascript functions, we automatically have the capability to do anything with painter operations that we can do with functions. For example, we can abstract the previous pattern Wave4 as
function Wave4(painter) {
var Wave2 = Besides(Wave(), Wave());
return Below(Wave2, Wave2);
}
We can also define recursive operations. Here is one that makes painters split and branch outwards towards the right
function RightSplit(painter, n) {
if (n === 0) {
return painter
} else {
var smaller = RightSplit(painter, n - 1);
return Besides(painter, Below(smaller, smaller));
}
}
We can produce balanced patterns by branching both upwards as well as towards the right
function CornerSplit(painter, n) {
if (n == 0) {
return painter;
} else {
// Create Top Left Corner
var up = UpSplit(painter, n - 1);
var topLeft = Besides(up, up);
// Create Bottom Right
var right = RightSplit(painter, n - 1);
var bottomRight = Below(right, right);
var corner = CornerSplit(painter, n - 1);
return Besides(Below(painter, topLeft),
Below(bottomRight, corner));
}
}
By placing four copies of a CornerSplit appropriately, we can obtain a pattern called SquareLimit, whose application to Wave is as follows:
function SquareLimit(painter, n){
var quarter = CornerSplit(painter, n);
var half = Besides(FlippedHorz(quarter), quarter);
return Below(FlippedVert(half), half);
}
Higher Order Operations
In addition to abstracting patterns of combining painters, we can work at a higher level, abstracting patterns of combining painter operations. That is, we can view the painter operations as elements to manipulate and can write means of combination for these elements - functions that take painter operations as arguments and create new painter operations.
For example, FlippedPairs and SquareLimit each arrange four copies of painter’s image in a square pattern; they differ only in how they orient the copies. Below you can see the FlippedPairs code and output.
One way to abstract this pattern of painter combination is with the following function, which takes four one-argument painter operations and produces a painter operation that transforms a given painter with those four operations and arranges the result in a square. tl, tr, bl, br are the transformations to apply to the top left copy, the top right copy, the bottom left copy and the bottom right copy respectively.
function SquareOfFour(tl, tr, bl, br){
var top = Besides(tl, tr);
var bottom = Besides(bl, br);
return Below(bottom, top);
}
The FlippedPairs can be defined in terms of SquareOfFour as follows:
Frames
Before we can show you how to implement painters and their means of combination, we must first consider frames. A frame can be described by three vectors - an origin vector and two edge vectors. The origin vector specifies the offset of the frame’s origin from some absolute origin in the plane, and the edge vectors specify the offset of the frame’s corners from its origin. If the edges are perpendicular, the frame will be rectangular. Otherwise the frame will be a more general parallelogram.
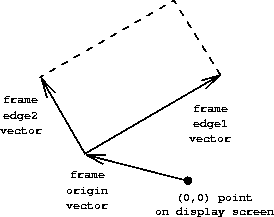
In accordance with data abstraction , we need not be specific yet about how frames are represented, other than to say that there is a constructor Frame, which takes three vectors and produces a frame, and three corresponding selectors getOrigin(), getEdge1(), getEdge2().
var Frame = function Frame() {
function Frame(ctx, origin, edge1, edge2) {
this.ctx = ctx;
this.origin = origin;
this.edge1 = edge1;
this.edge2 = edge2;
}
Frame.prototype.getOrigin = function () {
return this.origin;
};
Frame.prototype.getEdge1 = function () {
return this.edge1;
};
Frame.prototype.getEdge2 = function () {
return this.edge2;
};
Frame.prototype.getContext = function () {
return this.ctx;
};
return Frame;
}();
We will use coordinates in the unit square (0 <= x, y <= 1) to specify images. With each frame, we associate a frame co-ordinate map, which will be used to shit and scale images to fit the frame. The map transforms the unit square into the frame by mapping the vector v = (x, y) to the vector sum
Origin(Frame) + x.Edge_1(Frame) + y.Edge_2(Frame)
For example, (0,0) is mapped to the origin of the frame, (1,1) to the vertex diagonally opposite the origin, (0.5, 0.5) to the center of the frame. We can create a frame’s coordinate map with the following function:
var Helpers = {
generateFrameCoordinateMap: function (frame) {
return function (v) {
return frame.getOrigin()
.add(frame.getEdge1().scale(v.getX()))
.add(frame.getEdge2().scale(v.getY()))
}
}
};
Observe that applying generateFrameCoordinateMap to a frame returns a function that, given a vector, returns a vector. If the argument vector is the unit square, the result will be in the frame. For example,
generateFrameCoordinateMap(frame)(new Vector(0,0))
returns the same vector as
frame.getOrigin();
Painters
A painter is represented as a function that, given a frame as argument, draws a particular image shifted and scaled to fit the frame. That is to say that if p is a painter and f is a frame, then we produce p’s image in f by calling p with f as argument.
The details of how primitive painters are implemented depends on the particular characteristics of the graphics system and the type of image to be drawn. In an html context we can create a painter for line drawings such as the Wave painter seen previously as follows:
function LinePainter(lines) {
return function (frame) {
var transform = Helpers.generateFrameCoordinateMap(frame);
lines.forEach(function (l) {
frame.ctx.beginPath();
var tStart = transform(l.startSegment);
var tEnd = transform(l.endSegment);
frame.ctx.moveTo(tStart.getX(), frame.ctx.canvas.height - tStart.getY());
frame.ctx.lineTo(tEnd.getX(), frame.ctx.canvas.height - tEnd.getY());
frame.ctx.stroke();
});
}
}
The segments are given using coordinates with respect to the unit square. For each segment in the list, the painter transforms the segment endpoints with the frame coordinate map and draws a line between the transformed points.
Representing painters as functions erects a powerful abstraction barrier in the picture language. We can create and intermix all sorts of primitive painters, based on a variety of graphics capabilities. The details of their iimplementation do not matter. Any function can serve as a painter, provided that it takes a frame as argument and draws something scaled to fit the frame.
Transforming and combining painters
An operation on painters (such as FlippedVert or Besides) works by creating a painter that invokes the original painters with respect to frames derived from the argument frame. Thus, for example, FlippedVert does not have to know how a painter works in order to flip it - it just has to know how to turn a frame upside down. The flipped painter just used the original painter by in the inverted frame.
Painter operations are based on the function TransformPainter, which takes as arguments a painter and information on how to transform a frame and produces a new painter. The transformed painter, when called on a frame, transforms the frame and calls the origin painter on the transformed frame. The arguments to TransformPainter are points (represented as vectors) that specify the corners of the new frame: When mapped into the frame, the first point specifies the new frame’s origin and the other two specify the ends of its edges vectors. Thus arguments within the unit square specify a frame contained within the original frame.
function TransformPainter(painter, origin, corner1, corner2) {
return function (frame) {
var m = Helpers.generateFrameCoordinateMap(frame);
var newOrigin = m(origin);
var newCorner1 = m(corner1);
var newCorner2 = m(corner2);
var newFrame = new Frame(frame.ctx, newOrigin, newCorner1.sub(newOrigin), newCorner2.sub(newOrigin));
painter(newFrame);
}
}
Here is how to flip painter images vertically:
function FlippedVert(painter) {
return TransformPainter(
painter,
new Vector2(0.0, 1.0),
new Vector2(1.0, 1.0),
new Vector2(0.0, 0.0)
);
}
Using TransformPainter, we can easily define new transformations. For example we can define a painter that shrinks its image to the upper right quater of the frame it is given:
function ShrinkUpperRight(painter) {
return TransformPainter(
painter,
new Vector2(0.5, 0.5),
new Vector2(1.0, 0.5),
new Vector2(0.5, 1.0)
)
}
Other transformations rotate iamges couterclockwise by 90 degrees
function Rotate90(painter) {
return TransformPainter(
painter,
new Vector2(1.0, 0.0),
new Vector2(1.0, 1.0),
new Vector2(0.0, 0.0)
)
}
or squash images towards the center of the frame:
function SquashInwards(painter) {
return TransformPainter(
painter,
new Vector2(0.0, 0.0),
new Vector2(0.65, 0.35),
new Vector2(0.35, 0.65)
)
}
Frame transformation is also the key to defining means of combining two or more painters. The Besides function, for example, takes two painters, tranforms them to pain in the left and right halves of an argument frame respectively, and produces a new, compound painter. When the compound painter is given a frame, it calls the first transformed painter to paint in the left half of the frame and calls the second transformed painter to paint on the right half of the frame:
function Besides(painter1, painter2) {
var splitPoint = new Vector2(0.5, 0.0);
var paintLeft = TransformPainter(painter1,
new Vector2(0.0, 0.0),
splitPoint,
new Vector2(0.0, 1.0));
var paintRight = TransformPainter(painter2,
splitPoint,
new Vector2(1.0, 0.0),
new Vector2(0.5, 1.0));
return function (frame) {
paintLeft(frame);
paintRight(frame);
}
}
Observe how the painter data abstraction, and in particular the representation of painters as functions, makes Besides easy to implement. The Besides procedure need not know anything about the details of the component painters other than that each painter will draw something in its designated frame.
Levels of language for robust design
The picture langage exercises some of critical ideas about abstraction with procedures and data. The fundamental data abstractions, painters, are implemented using functional representations, which enables the language to handle different basic drawing capabilities in a uniform way. The means of combination satisfy the closure property, which permits us to easily build up complex designs. Finally, all the tools for abstracting functions are available to us for abstracting means of combination for painters.
We have also obtained a glimpse of another crucial idea about language and program design. This is the approach of stratified design, the notion that a complex system should be structures as a sequence of levels that are described using a sequence of languages. Each level is constructed by combining parts that are regarded as primitive at the level, and the parts constructed at each level are used as primites at the next level. The language used at each level of stratified design has primitives, and means of abstraction appropriate to the level of detail.
Stratified design helps make programs robust, that is, it makes it likely that small changes in a specification will require corresponding small changes in the program. For instance, suppose we want to change the images based on Wave. We could work at the lowest level to change the appearance of the Wave element; we could work at the middle level to change the way the CornerSplit replicates the Wave; we could work at the highest level to change how the SquareLimit arranges the four copies of the corner. In general, each level of a stratified design provides a different vocabulary for expressing the characteristics of the system, and a different kind of ability to change it.