Lambda Calculus is Dead! Long live Lambda Calculus!

Introduced by Alonzo Church in the 1930s, $\lambda$-calculus can be considered as the smallest computation programming language of the world. Reading through the various tutorials one can find various examples which showcase its universality; addition, conditional operators, equality and inequality and recursion. One thing which always intrigued me is how applicable is $\lambda$-calculus to everyday problems such as finding the set of URLs in a sitemap or a set of alternate language urls? The question is obviously rhetorical since we know that $\lambda$-calculus is Turing complete! Can we model a “modern” problem in terms of $\lambda$-calculus and will such a problem still feel natural? The answer is yes! In this post we are going to apply $\lambda$-calculus in an SEO domain, specifically to construct a Sitemap and to find the hreflang for a language.
$\lambda$-Calculus
The central concept in $\lambda$-calculus is an expression. An expression is defined recursively as follows (not pure $\lambda$-calculus):
\[\begin{eqnarray*} \texttt{<expression>}&=&\texttt{<name>}|\texttt{<cons>}|\texttt{<function>}|\texttt{<application>}\\ \texttt{<function>}&=&\lambda\texttt{<name>}.\texttt{<expression>}\\ \texttt{<application>}&=&\texttt{<expression>}\texttt{<expression>} \end{eqnarray*}\]where
name, also referred to as a variable, is an identifier which for our purposes will be any sequence of italic lowercase letters e.g. lang, slug.consis a constant which for our purposes will be represented by a sequence of lowercase letters e.g.en,fi,sv.
Having defined an expression let us look at some examples:
\[\begin{eqnarray*} &\texttt{en}\\ &\texttt{sv}\\ &\textit{lang}\\ &\lambda\textit{lang}. \textit{lang}\\ &(\lambda\textit{lang}.\textit{lang})(\lambda\textit{slug}.\textit{slug})\\ &(\lambda\textit{lang}.\textit{lang})\texttt{en} \\ \end{eqnarray*}\]Notation-wise we will use the following rules:
- Variables are listed after the $\lambda$ e.g. lang is a variable in $\lambda\textit{lang}.\textit{lang}$
- An application is always associated to the left such that $E_1 \dots E_{n} \equiv (((E_1 E_2) E_3) \dots E_n)$
- $\lambda$ binds to the right as far as possible: $\lambda \textit{l}.\textit{l} \textit{l} \equiv \lambda \textit{l}.(\textit{l} \textit{l}) \not\equiv (\lambda \textit{l}.\textit{l})\textit{l}$
- Outermost parenthesis are omitted: $E_1 \ldots E_2 \equiv (E_1 \ldots E_2)$
Free and Bound Variables
In $\lambda$-calculus all names are local to definition. In the function $\lambda \textit{x}.\textit{x}$ we say that $\textit{x}$ is “bound” since its occurrence in the body of the definition is preceded by $\lambda \textit{x}$. A name not preceded by $\lambda$ is called a “free variable”.
The set of free variables can be defined recursively:
\[\begin{eqnarray*} &FV(<cons>) &=& \emptyset \\ &FV(<name>) &=& {<name>} \\ &FV(<exp_1> <exp_2>) &=& FV(<exp_1>) \cup FV(<exp_2>) \\ &FV(\lambda <name>. <exp>) &=& FV(<exp>) \setminus \{<name>\} \end{eqnarray*}\]Similarly, the set of bound variables can be defined recursively:
\[\begin{eqnarray*} &BV(<cons>) &=& {<cons>} \\ &BV(<name>) &=& \emptyset \\ &BV(<exp_1> <exp_2>) &=& BV(<exp_1>) \cup BV(<exp_2>) \\ &BV(\lambda <name>. <exp>) &=& BV(<exp>) \cup \{<name>\} \end{eqnarray*}\]$\beta$-Reduction
In $\lambda$-calculus there is one computational rule called $\beta-$reduction: $((\lambda\textit{x}.s)\texttt{t})$ can be reduced to $\textit{s}[\texttt{t}/\textit{x}]$, the result of replacing the arguments $\texttt{t}$ for the formal parameter $\textit{x}$ in $s$. Note: It is assumed that no substitution will mix free and bound identifiers and hence we will omit the discussion of $\alpha$-reduction. Some examples are:
\[\begin{eqnarray*} ((\lambda \textit{lang}.\textit{lang})\texttt{en}) \rightarrow_{\beta} \texttt{en} \\ ((\lambda\textit{x}.\textit{x})(\lambda\textit{x}.\textit{x})) \rightarrow_{\beta} (\lambda\textit{x}.\textit{x}) \end{eqnarray*}\]A more complex example would be the following:
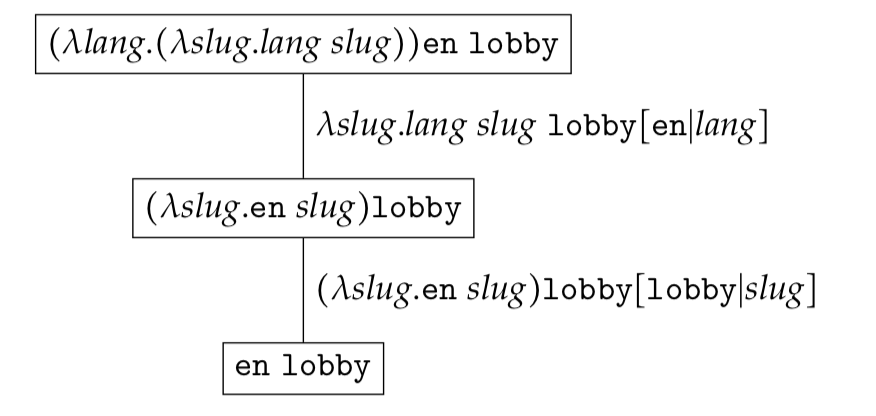
\[\begin{eqnarray*} &((\lambda \textit{lang}. (\lambda \textit{slug}. \textit{lang} \ \textit{slug})) `en`)\texttt{lobby} \\ &((\lambda \boxed{\textit{lang}}. (\lambda \textit{slug}.\boxed{\textit{lang}}\textit{slug}))\boxed{\texttt{en}})\texttt{lobby} \\ &(\lambda \textit{slug}.\texttt{en}\ \textit{slug})\texttt{lobby} \\ &(\lambda \boxed{\textit{slug}}.\texttt{en}\ \boxed{\textit{slug}})\boxed{\texttt{lobby}} \\ &(\texttt{en}\ \texttt{lobby}) \\ \end{eqnarray*}\]Some $\lambda-$expressions have a non-deterministic reduction. Let us take as an example the $\lambda$-expression $(\lambda x.x x)((\lambda y.y)z)$. This $\lambda$-expression has two possible reductions
\[\begin{eqnarray*} & (\lambda x.x x)((\lambda y.y)z) \\ & (\lambda x.x x)(\lambda z.z) \\ & (\lambda z.z)(\lambda z.z) \\ & (\lambda z.z) \end{eqnarray*}\]and
\[\begin{eqnarray*} & (\lambda x.x x)((\lambda y.y)z) \\ & ((\lambda y.y)z)((\lambda y.y)z) \\ & (\lambda z.z)(\lambda z.z) \\ & (\lambda z.z) \end{eqnarray*}\]On the other end of the spectrum we find expressions that do not have a single reduction sequence. As an example consider
\[\begin{eqnarray*} (\textit{x}(\lambda \textit{y}.\textit{y})) \end{eqnarray*}\]For the purposes of our discussion we will only consider $\lambda$-expressions of the form
\[\begin{equation*} (\lambda n_1\lambda n_2\ldots\lambda n_{k} \cdot n_1n_2\ldots n_{k})c_1c_2\ldots c_{k} \end{equation*}\]where $n_1\ldots n_{k}$ are the parameters of the lambda functions and $c_1\ldots c_{k}$ are the arguments of the function. Each individual argument $c_{k}$ can be either a name or constant. It can be shown that expressions of this form are deterministic and fully normalised (cannot be reduced further). Specifically, it will take $k$ $\beta-$reductions to normalise the $\lambda$-expression.
\[\begin{eqnarray*} & (\lambda n_1\lambda n_2\ldots\lambda n_{k} \cdot n_1n_2\ldots n_{k})c_1c_2\ldots c_{k} \\ & (\lambda n_2\ldots\lambda n_{k} \cdot c_1n_2\ldots n_{k})c_2\ldots c_{k}[c_1|n_1] \\ & (\lambda n_3\ldots\lambda n_{k} \cdot c_1c_2\ldots n_{k})c_3\ldots c_{k}[c_2|n_2] \\ & \dots \\ & (c_1c_2\ldots c_{k})[c_{k}|n_{k}] \\ \end{eqnarray*}\]Context
Given a $\lambda$-expression of the form
\[\begin{equation*} (\lambda n_1\lambda n_2\ldots\lambda n_{k} \cdot n_1n_2\ldots n_{k})c_1c_2\ldots c_{k} \end{equation*}\]we will refer to the sequence of reductions $c_1c_2\ldots c_{k}$ as the context of the $\lambda-$expression. In this context the item $c_{k}$ is called a variable. The variable $c_{k}$ can take on two possible values: a name or a constant. If $c_{k}$ is a name we will say that the variable $c_{k}$ is a free variable since the normalised expression will contain such a name $c_{k}$ in the set of free variables. If $c_{k}$ is a constant we will say that the variable $c_{k}$ is a bound variable since the normalised expression will contain such a constant $c_{k}$ in the set of bound variables. As an example let us consider the following:
In this case the variable $c_1$ is the name $\textit{a}$ and the variable $c_2$ is the constant $\texttt{lobby}$. The normalised expression is $\textit{a}\ \texttt{lobby}$. It is clear that the free variable $\textit{a}$ is a free variable in the normalised $\lambda-$expression $\textit{a}\ \texttt{lobby}$ and that $\texttt{lobby}$ is a bound variable.
When all $c_1\ldots c_{k}$ variables are free we will refer to the lambda expression as a free lambda expression. When all $c_1\ldots c_{k}$ variables are bound we will refer to the lambda expression as a bound lambda expression. When the context contains a mix of free and bound variables we will refer to the lambda expression as a partial lambda expression.
Given a context $c_1\ldots c_{k}$, the $\lambda-$expression required to normalise to the context is
\[(\lambda n_1\ldots\lambda n_{k} \cdot n_1\ldots n_{k})c_1\ldots c_{k}\]Similarly, given a normalised expression $c_1\ldots c_{k}$ one can always find the source context and the source $\lambda-$expression which reduced to the normalised expression. To make such a conversion explicit we will use the function $\omega(c_1\ldots,c_{k})$
\[\begin{eqnarray*} \omega(c_1\ldots c_{k}) &=& (\lambda n_1\ldots\lambda n_{k} \cdot n_1\ldots n_{k})c_1\ldots c_{k} \end{eqnarray*}\]Expression Tree
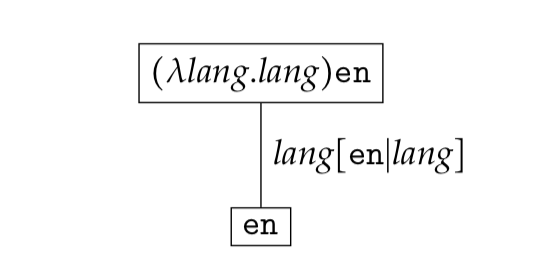
Starting with a $\lambda$-expression at the root, one can visualise all the reduction steps leading to the normalised expression in a tree. As an example let us consider how the reduction sequence for $(\lambda \textit{lang}. \textit{lang}) \texttt{en}$ can be represented.
A more complex example would be the following
In general, the generic $\lambda-$expression
\[\begin{eqnarray*} & (\lambda n_1\lambda n_2\ldots\lambda n_{k} \cdot n_1n_2\ldots n_{k})c_1c_2\ldots c_{k} \\ \end{eqnarray*}\]can be represented as follows

Notation-wise we will use $\psi((\lambda n_1\ldots\lambda n_{k} \cdot n_1\ldots n_{k})c_1\ldots c_{k})$ or $\psi(\omega(c_1\ldots c_{k}))$ to refer to the sequence of reductions i.e. expression tree.
Expression Sets
Reduction trees discussed in the previous section represent the normalisation steps for a given expression $\omega(c_1c_2\ldots c_{k})$ where $c_1,\ldots,c_{k}$ is in a given configuration. If $c_{1} \in \mathcal{C}_{1}, c_{2} \in \mathcal{C}_{2}, \ldots, c_{k} \in \mathcal{C}_{k}$ we can build the set of all expression trees by normalising all expressions in the set
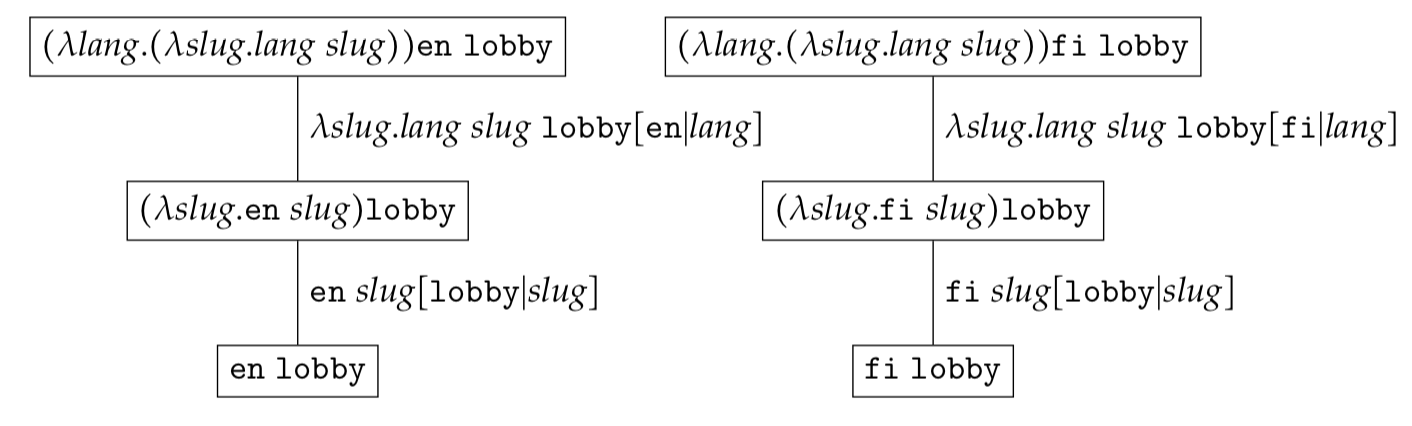
\[\begin{eqnarray*} \mathcal{RS} = \{ \omega(c_1c_2\ldots c_{k}) | (c_1, c_2, \ldots, c_{k}) \in \mathcal{C}_{1} \times \mathcal{C}_{2} \times \ldots \times \mathcal{C}_{k}\} \end{eqnarray*}\]You can think of $\mathcal{C}_{k}$ as the type for variable $c_{k}$. As an example let us consider the expression $((\lambda \textit{lang}. (\lambda \textit{slug}. \textit{lang}\ \textit{slug}))c_1c_2$. Where $c_1 \in \{ \texttt{en}, \texttt{fi} \}$ and $c_2 \in \{ \texttt{lobby} \}$. The reduction set $\mathcal{RS}$ would contain two trees
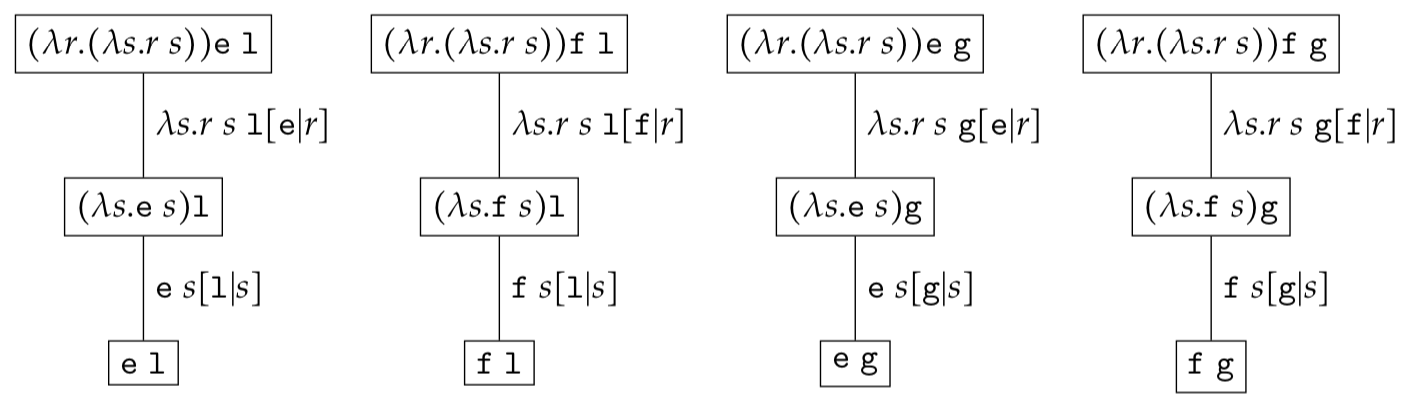
If $c_1 \in \{\texttt{e}, \texttt{f}\}$ and $c_2 \in \{\texttt{l}, \texttt{g}\}$ the reduction set $\mathcal{RS}$ would contain four trees
Given that each expression tree has only one reduction sequence to normalisation we will merge all expression trees in a single tree by omitting the context. As an example let us consider the $\lambda-$expression set
\[\begin{eqnarray*} & (\lambda \textit{lang}. (\lambda \textit{slug}. \textit{lang}\ \textit{slug}))c_1c_2 \end{eqnarray*}\]where $c_1 \in \{ \texttt{en},\texttt{fi}\}$ and $c_2 \in \{ \texttt{lobby}, \texttt{games}\}$.
The expression set can be represented as
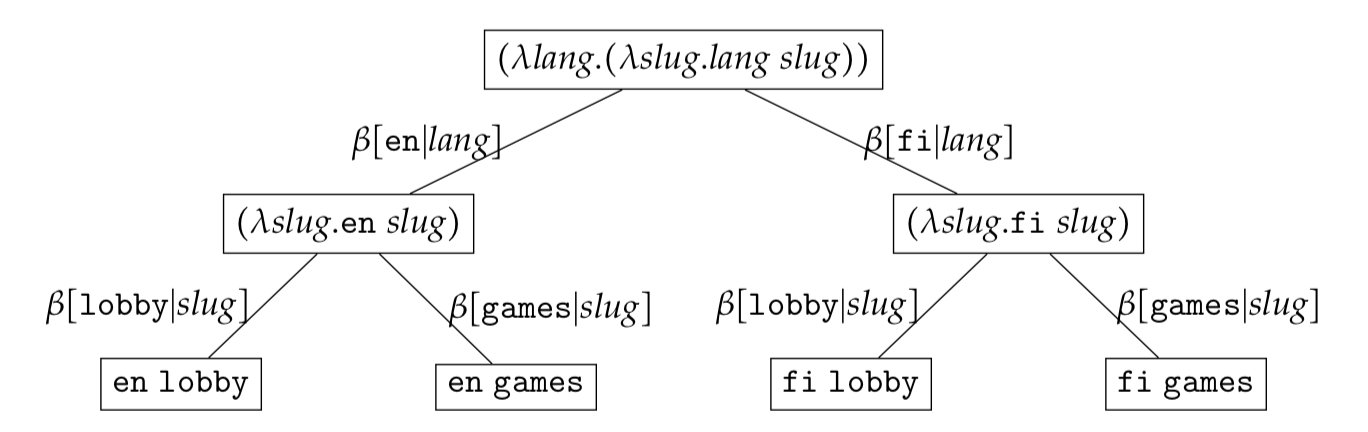
It is important to note that an expression set tree is just a visualisation aide. Mentally, one should always expand each node in the tree to the set of $\lambda-$expressions. At each level the set of $\lambda-$expressions being represented can be found by mapping all descendant leaf-nodes using $\omega(c_1c_2\ldots c_{k})$ defined in the previous section. As an example the root node in the expression set $\lambda \textit{l}.\lambda \textit{s}.\textit{l}\ \textit{s}$ has four descendant leaf nodes
\[\begin{eqnarray*} &\{\omega(\texttt{en}\ \texttt{lobby}),\omega(\texttt{fi}\ \texttt{lobby}),\omega(\texttt{en}\ \texttt{games}),\omega(\texttt{fi}\ \texttt{games})\} \end{eqnarray*}\]and hence represents the set
\[\begin{eqnarray*} &\{\lambda \textit{l}.\lambda \textit{s}.\textit{l}\textit{s}\ \texttt{en}\ \texttt{lobby}, \lambda \textit{l}.\lambda \textit{s}.\textit{l}\textit{s}\ \texttt{fi}\ \texttt{lobby}, \lambda \textit{l}.\lambda \textit{s}.\textit{l}\textit{s}\ \texttt{en}\ \texttt{games}, \lambda \textit{l}.\lambda \textit{s}.\textit{l}\textit{s}\ \texttt{fi}\ \texttt{games} \} \end{eqnarray*}\]Free/Bound/Partial Reduction Sets
Leaf nodes in a reduction set represent normalised expressions. If all leaf expressions (normalised expressions) are bound expressions we say that the reduction set is a bound reduction set. The example below illustrates a bound reduction set.
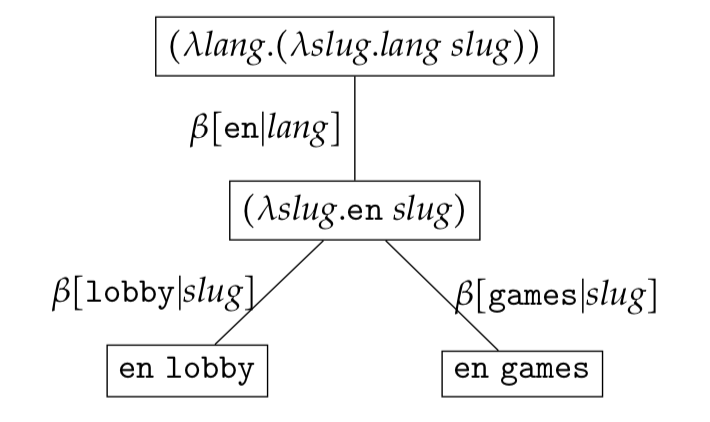
If some normalised expressions are bound we say that the reduction set is a partial reduction set. The example below illustrates a partial reduction set.
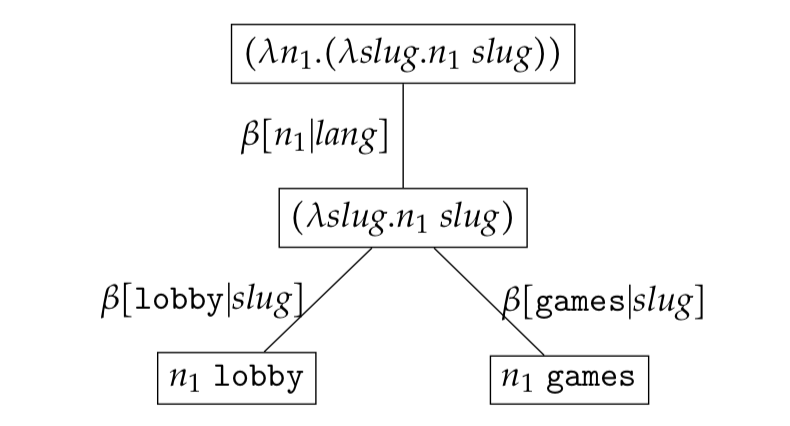
If no normalised expressions are bound - that is all leaf expressions are free - we say that the reduction set is a free reduction set. The example below illustrates a free reduction set.
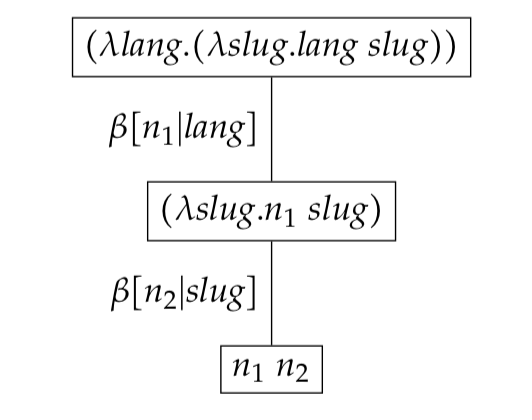
Serialisation and de-serialisation
Serialisation
Given a $\lambda-$expression of the form
\[\begin{eqnarray*} (\lambda n_1\lambda n_2\lambda n_3\ldots\lambda n_{k} \cdot n_1n_2n_3\ldots n_{k})c_1c_2c_3\ldots c_{k} \end{eqnarray*}\]we can serialise the normalised reduction $c_1\ldots c_{k}$ by means of a bijective function $f$ which takes a context configuration and maps it to a string $s$. The function $f$ has to be bijective, as later on, we will need to deserialise the string back to the context.
\[\begin{eqnarray*} f: \mathcal{C}_{1} \times \ldots \times \mathcal{C}_{k} \rightarrow \mathcal{S} \end{eqnarray*}\]One implementation of serialisation function $f$ is to join the context using the / character. As we have two types of variables, free and bound, we need to distinguish between these different types so during deserialisation, the context can be correctly reconstructed. In order to distinguish between free and bound variables we will prefix free variables with the colon prefix.
Let’s serialise the following expression
\[\begin{eqnarray*} (\lambda \textit{n}_1. (\lambda \textit{n}_2. \textit{n}_1\ \textit{n}_2) \textit{lang})\texttt{slots} \end{eqnarray*}\]The normalised context for this expression is
\[\begin{eqnarray*} &c_1=\textit{lang}\\ &c_2=\texttt{slots} \end{eqnarray*}\]The result of serialising the above expression is
\[\begin{eqnarray*} f(\textit{lang }\texttt{slots}) = /\colon lang/slots/ \end{eqnarray*}\]One other implementation of a serialisation function is $f_{int}$ which takes a context and serialises the context into an internationalised string. As an example consider \(\begin{eqnarray*} (\lambda \textit{n}_1. (\lambda \textit{n}_2. \textit{n}_1\ \textit{n}_2) \texttt{fi})\texttt{slots} \end{eqnarray*}\)
The context for this expression is
\[\begin{eqnarray*} &c_1=\texttt{fi}\\ &c_2=\texttt{slots} \end{eqnarray*}\]The result of serialising the above expression is \(\begin{equation*} f_{int}(\texttt{fi slots}) = /fi/kolikkopelit/ \end{equation*}\)
where the constant slots in Finnish is serialised to kolikkopelit.
Deserialisation
Deserialisation maps a string representation back to the context.
\[\begin{eqnarray*} \bar{f}: \mathcal{S} \rightarrow \mathcal{C}_{1} \times \ldots \times \mathcal{C}_{k} \end{eqnarray*}\]One implementation of the $\bar{f}$ function obtains the original context using the context extraction function $ce$
\[\begin{eqnarray*} ce(/c_1/c_2/\dots /c_k/) = c_1c_2\dots c_k \end{eqnarray*}\]and reconstructs the original expression using the $\omega$ function
\[\begin{eqnarray*} \bar{f}(/c_1/c_2/\dots /c_k/)&=&\omega(ce(/c_1/c_2/\dots /c_k)) \end{eqnarray*}\]Given a serialisation
\[\begin{eqnarray*} &/\colon lang/lobby/ \\ &\bar{f}(/\colon lang/lobby/) = (\lambda n_1\lambda n_2\cdot n_1n_2)\textit{lang}\ \texttt{lobby} \end{eqnarray*}\]Search
Search enables us to find a particular expression tree in an expression set. In order to create a search function we will first define a match function for expressions. The match function takes a source (source) $\lambda$-expression and a search $\lambda$-expression (se) and returns a true if
\[\begin{eqnarray*} match(source, se) = BV(source) \supseteq BV(se) \end{eqnarray*}\]As an example let us match $\lambda l.\texttt{en}$ to itself
\[\begin{eqnarray*} & match(\lambda l.\texttt{en},\ \lambda l.\texttt{en}) \\ & BV(\lambda l.\texttt{en}) \supseteq BV(\lambda l.\texttt{en}) \\ & \{ l, \texttt{en} \} \supseteq \{ l, \texttt{en} \} \\ & true \end{eqnarray*}\]Having defined match for expression we will move up the abstraction hierarchy and define matching on expression trees. Let’s overload the $match$ function so that it now takes a source expression tree and a search expression tree and calls match on the source and search expression trees.
Let us $match$ the expression tree $\psi(((\lambda \textit{l}. (\lambda \textit{s}. \textit{l}\ \textit{s})) \texttt{en})\texttt{lobby})$ to itself.
\[\begin{eqnarray*} & match(\psi(\omega(\texttt{en lobby})),\ \psi(\omega(\texttt{en lobby}))) \\ & match(\texttt{en lobby},\ \texttt{en lobby}) \\ & BV(\texttt{en lobby}) \supseteq BV(\texttt{en lobby}) \\ & \{ \texttt{en}, \texttt{lobby} \} \supseteq \{ \texttt{en}, \texttt{lobby} \} \\ & true \end{eqnarray*}\]Having defined match for expression tree we will move up (once again) the abstraction hierarchy and define a $search$ function for expression sets. Since the expression set $\mathcal{RS}$ represents a set of expression trees, searching through an expression set is simply the act of matching each element of the expression set with the search expression tree se.
\[\begin{equation*} \mathcal{RS}_{match}(se) = \{ t \in \mathcal{RS}, match(t, se) \} \end{equation*}\]Search Properties
In this section we shall look at two search properties: the search identity and freed context identity.
Search identity
The number of normalised expression nodes a set can have is dependant on the context. Specifically it is the cartesian product of all contexts $\mathcal{C}_{1}\ldots \mathcal{C}_{k}$. The set of normalised expressions in a bound expression set $\mathcal{RS}$ implies that there is one and only one reduction to any $c’ \in \mathcal{C}_{1} \times \ldots \times \mathcal{C}_{k}$. Thus, any search starting from a bound context $c’$ will find the same normalised node $c’$. We call this the search identity.
Let’s for instance search for
\[\begin{eqnarray*} \psi((\lambda \textit{l}. \lambda \textit{s}. \textit{l}\ \textit{s})\texttt{en}\ \texttt{lobby}) \end{eqnarray*}\]on the expression set
\[\begin{eqnarray*} \mathcal{RS} = (\lambda \textit{l}. \lambda \textit{s}. \textit{l}\ \textit{s}){c}_1{c}_2 \end{eqnarray*}\]where $c_1 \in \{\texttt{en}, \texttt{fi}\}$ and $c_2 \in \{\texttt{lobby}, \texttt{games}\}$.
\[\begin{eqnarray*} search(\mathcal{RS}, \psi((\lambda \textit{l}. \lambda \textit{s}. \textit{l}\ \textit{s})\texttt{en}\ \texttt{lobby})) &=& \psi((\lambda \textit{l}. \lambda \textit{s}. \textit{l}\ \textit{s})\texttt{en}\ \texttt{lobby}) \end{eqnarray*}\]The individual $match$ reductions are
\[\begin{eqnarray*} & match(\psi(\omega(\texttt{fi lobby})),\ \psi(\omega(\texttt{en lobby}))) \\ & match(\texttt{fi lobby},\ \texttt{en lobby}) \\ & BV(\texttt{fi lobby}) \supseteq BV(\texttt{en lobby})\\ & \{ \texttt{fi}, \texttt{lobby} \} \supseteq \{ \texttt{en}, \texttt{lobby} \} \\ & false \end{eqnarray*}\] \[\begin{eqnarray*} & match(\psi(\omega(\texttt{fi games})),\ \psi(\omega(\texttt{en lobby}))) \\ & match(\texttt{fi games},\ \texttt{en lobby}) \\ & BV(\texttt{fi games}) \supseteq BV(\texttt{en lobby}) \\ & \{ \texttt{fi}, \texttt{games} \} \supseteq \{ \texttt{en}, \texttt{lobby} \} \\ & false \end{eqnarray*}\] \[\begin{eqnarray*} & match(\psi(\omega(\texttt{en games})),\ \psi(\omega(\texttt{en lobby}))) \\ & match(\texttt{en games},\ \texttt{en lobby}) \\ & BV(\texttt{en games}) \supseteq BV(\texttt{en lobby}) \\ & \{ \texttt{en}, \texttt{games} \} \supseteq \{ \texttt{en}, \texttt{lobby} \} \\ & false \end{eqnarray*}\] \[\begin{eqnarray*} & match(\psi(\omega(\texttt{en lobby})),\ \psi(\omega(\texttt{en lobby}))) \\ & match(\texttt{en lobby},\ \texttt{en lobby}) \\ & BV(\texttt{en lobby}) \supseteq BV(\texttt{en lobby}) \\ & \{ \texttt{en}, \texttt{lobby} \} \supseteq \{ \texttt{en}, \texttt{lobby} \} \\ & true \end{eqnarray*}\]Freed context search
Searching for a bound expression tree will not yield meaningful results. In general we are interested in searching for expression trees which are similar to a search expression tree. In order to generalise a normalised expression tree we will substitute one or more constants with free variables. Consider the following expression set
\[\begin{eqnarray*} \mathcal{RS} = (\lambda \textit{l}. \lambda \textit{s}. \textit{l}\ \textit{s}){c}_1{c}_2 \end{eqnarray*}\]In general one would search for a bound expression tree to uniquely identify the expression tree within an expression set
where $c_1 \in \{\texttt{en}, \texttt{fi}\}$ and $c_2 \in \{\texttt{lobby}, \texttt{games}\}$.
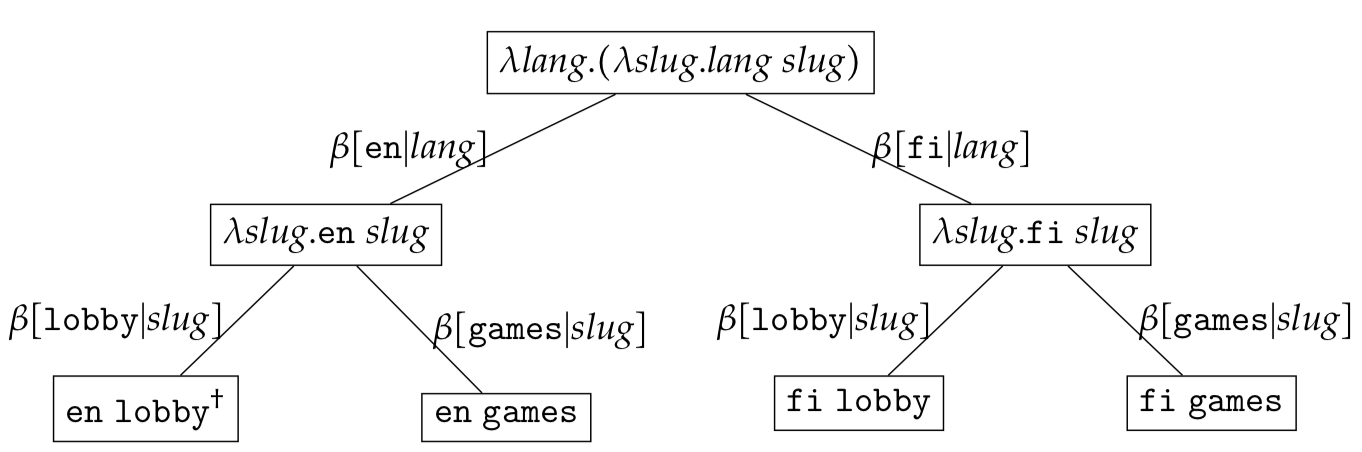
The normalised reduction for the node with the $\dagger$ symbol is $\texttt{en}\ \texttt{lobby}$. In order to retrieve similar nodes one needs to substitute constants with free variables. Such a substitution marginalises all constant values for the given variable $c_{k}$ making such a variable (in the context) irrelevant to the search. For instance in order to find similar $\texttt{lobby}$ expression trees, we retain the bound $\texttt{lobby}$ constant and replace the $\texttt{en}$ value with the free variable $\ast$. Searching for the expression tree $\psi(\lambda \textit{lang}. (\lambda \textit{slug}. \textit{lang}\ \textit{slug})\ast\ \texttt{lobby})$ will yield
The individual $match$ reductions are
\[\begin{eqnarray*} & match(\psi(\omega(\texttt{fi lobby})),\ \psi(\omega(\ast\ \texttt{lobby}))) \\ & match(\texttt{fi lobby},\ \ast\ \texttt{lobby}) \\ & BV(\texttt{fi lobby}) \supseteq BV(\ast\ \texttt{lobby}) \\ & \{ \texttt{fi}, \texttt{lobby} \} \supseteq \{ \texttt{lobby} \} \\ & true \end{eqnarray*}\] \[\begin{eqnarray*} & match(\psi(\omega(\texttt{fi games})),\ \psi(\omega(\ast\ \texttt{lobby}))) \\ & match(\texttt{fi games},\ \ast\ \texttt{lobby}) \\ & BV(\texttt{fi games})) \supseteq BV(\ast\ \texttt{lobby}) \\ & \{ \texttt{fi}, \texttt{games} \} \supseteq \{ \texttt{lobby} \} \\ & false \end{eqnarray*}\] \[\begin{eqnarray*} & match(\psi(\omega(\texttt{en lobby})),\ \psi(\omega(\ast\ \texttt{lobby}))) \\ & match(\texttt{en lobby},\ \ast\ \texttt{lobby}) \\ & BV(\texttt{en lobby}) \supseteq BV(\ast\ \texttt{lobby}) \\ & \{ \texttt{en}, \texttt{lobby} \} \supseteq \{ \texttt{lobby} \} \\ & true \end{eqnarray*}\] \[\begin{eqnarray*} & match(\psi(\omega(\texttt{en games})),\ \psi(\omega(\ast\ \texttt{lobby}))) \\ & match(\texttt{en games},\ \ast\ \texttt{lobby}) \\ & BV(\texttt{en games}) \supseteq BV(\ast\ \texttt{lobby}) \\ & \{ \texttt{en}, \texttt{games} \} \supseteq \{ \texttt{lobby} \} \\ & false \end{eqnarray*}\]Nothing! Give me Nothing!
Given the $\lambda$-expression
\[\begin{eqnarray*} (\lambda n_1\lambda n_2\lambda n_3\ldots\lambda n_{k} \cdot n_1n_2n_3\ldots n_{k})c_1c_2c_3\ldots c_{k} \end{eqnarray*}\]there may be cases where the context $c_k$ is undefined or nothing. We will represent nothing using the token constant $\varnothing$. We require that the types $\mathcal{C}_{k}$ include a dummy bound value $\varnothing$ to represent nothing. A configuration $c_1,\ldots,c_{k}$ is considered valid if
\[\begin{eqnarray*} \exists c_i.\ c_i=\emptyset\ |\ \forall c_{j}.c_{j}=\emptyset, j>i \end{eqnarray*}\]Informally, this requires that if a variable in a particular position within a configuration is $\varnothing$, all subsequent variables within the configuration need to be $\varnothing$.
As an example, let us consider the $\lambda$-expression
\[\begin{eqnarray*} (\lambda a. \lambda b. \lambda c. abc)c_1c_2c_3 \end{eqnarray*}\]where
\[\begin{eqnarray*} & c_1 \in \{\texttt{a}, \texttt{b}\} \\ & c_2 \in \{\texttt{c} \} \\ & c_3 \in \{\texttt{d} \} \\ \end{eqnarray*}\]In order to introduce nothing, we will add the constant $\varnothing$ to all type sets
\[\begin{eqnarray*} & c_1 \in \{\texttt{a}, \texttt{b}, \varnothing \} \\ & c_2 \in \{\texttt{c}, \varnothing\} \\ & c_3 \in \{\texttt{d}, \varnothing\} \\ \end{eqnarray*}\]and restrict the configuration $c_1c_2c_3$ to be in the set
\[\begin{eqnarray*} \{\texttt{a}\texttt{c}\texttt{d}, \texttt{b}\texttt{c}\texttt{d},\ \texttt{a}\texttt{c}\varnothing, \texttt{b}\texttt{c}\varnothing, \texttt{a}\varnothing\varnothing, \texttt{b}\varnothing\varnothing, \varnothing\varnothing\varnothing \} \\ \end{eqnarray*}\]$\varnothing$ does not affect $\beta-$reduction, it is after all a constant. As an example let us consider
We will typically omit $\varnothing$ from the expression set for clarity.
Search including nothing
As the $\varnothing$ is a constant, search does not need to be modified. Lets search for the expression tree $\psi(\omega({\texttt{en }\varnothing}))$ in the expression set
\[\begin{eqnarray*} \mathcal{RS}&=&\lambda \textit{lang}. (\lambda \textit{slug}. \textit{lang}\ \textit{slug}) \end{eqnarray*}\]where $lang \in \{\texttt{en},\ \varnothing\}$ and $slug \in \{\texttt{lobby},\ \varnothing\}$.
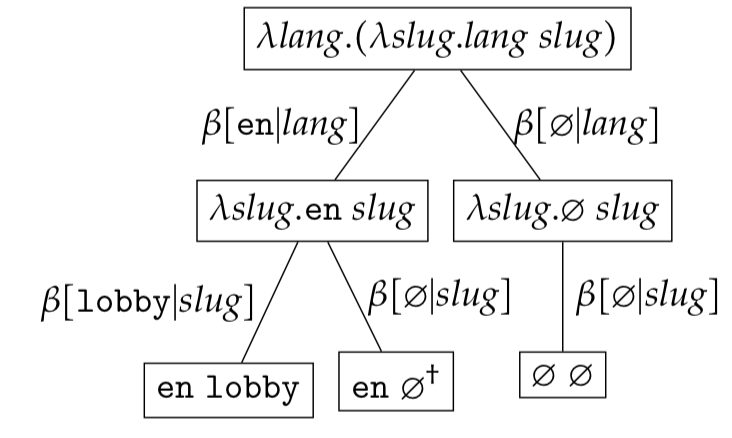
The individual $match$ reductions are
\[\begin{eqnarray*} & match(\psi(\omega(\texttt{en lobby})),\ \psi(\omega(\texttt{en }\varnothing))) \\ & match(\texttt{en lobby},\ \texttt{en }\varnothing) \\ & BV(\texttt{en lobby}) \supseteq BV(\texttt{en }\varnothing) \\ & \{ \texttt{en, lobby} \} \supseteq \{ \texttt{en }\varnothing \} \\ & false \end{eqnarray*}\] \[\begin{eqnarray*} & match(\psi(\omega(\texttt{en } \varnothing)),\ \psi(\omega(\texttt{en }\varnothing))) \\ & match(\texttt{en } \varnothing,\ \texttt{en }\varnothing) \\ & BV(\texttt{en }\varnothing) \supseteq BV(\texttt{en }\varnothing)\\ & \{ \texttt{en }\varnothing \} \supseteq \{ \texttt{en }\varnothing \} \\ & true \end{eqnarray*}\] \[\begin{eqnarray*} & match(\psi(\omega(\varnothing\ \varnothing)),\ \psi(\omega(\texttt{en }\varnothing))) \\ & match(\varnothing\ \varnothing,\ \texttt{en }\varnothing) \\ & BV(\varnothing\ \varnothing) \supseteq BV(\texttt{en }\varnothing) \\ & \{ \varnothing\ \varnothing \} \supseteq \{ \texttt{en }\varnothing \} \\ & false \end{eqnarray*}\]This comes as no surprise due to the search identity! Note that $\psi(\omega(\varnothing\ \texttt{lobby}))$ is not included in $\mathcal{RS}$ since this would violate
\[\begin{eqnarray*} \exists c_i.\ c_i=\emptyset\ |\ \forall c_{j}.c_{j}=\emptyset, j>i \end{eqnarray*}\]Integrating this with the Content Management System
In this section we shall discuss how the $\lambda$-calculus can be applied to solve two SEO problems: getting all the paths of the site and getting a path’s alternates in other languages.
Constructing the Partial Expression Set
Constructing an internationalised sitemap can be translated to the problem of serialising a bound expression set. But how does one construct such a bound expression set? All URLs on our website are saved in a Content Management System (CMS) and follow one of the following forms:
\[\begin{eqnarray*} &\texttt{/:lang/}\\ &\texttt{/:lang/slots/}\\ &\texttt{/:lang/slots/:slug/} \end{eqnarray*}\]One can interpret the above URLs as a serialisation originating from the expression set
\[\begin{eqnarray*} (\lambda n_{1}. \lambda n_{2}. \lambda n_3. n_{1}n_{2}n_{3}) c_{1}c_{2}c_{3} \end{eqnarray*}\]where $c_{1}=\textit{lang}$, $c_{2} \in \{ \texttt{slots}, \varnothing \}$ and $c_{3}=\textit{slug}$.
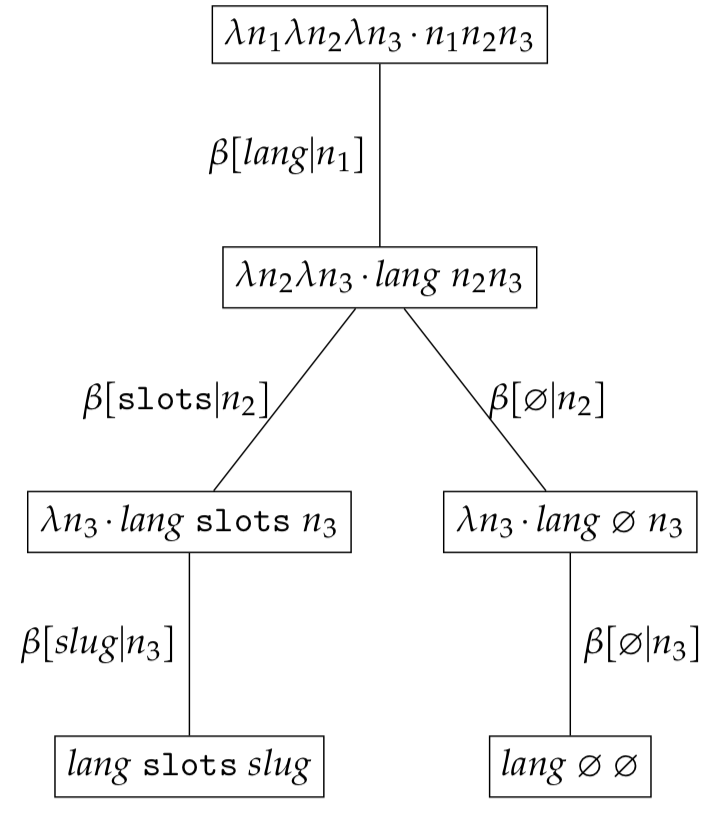
Such an expression set is a partial expression set and needs to be bound in order to retrieve a site’s sitemap. Recall from earlier that free variables represent a marginalisation of constants for a particular type $\mathcal{C}_{k}$. In this case lang represents a marginalisation of all constants of type $\mathcal{C}_{lang}$ and $\textit{slug}$ represents a marginalisation of all constants of type $\mathcal{C}_{slug}$. Resolvers provide a means of finding the set of constants $c_{k}$ for a type $\mathcal{C}_{k}$ when $c_{k}$ is a free variable.
Constructing the Bound Expression Set - Resolvers
A resolver function $r$ is a function which takes a context $c_{k}$ and returns the set of all possible bound values $\mathcal{C}_{k}$. This is required when the value $c_{k}$ has been marginalised by a free variable.
\[\begin{equation*} r(c_{k}) = \mathcal{C}_{k} \end{equation*}\]To convert the partial expression set
\[\begin{eqnarray*} (\lambda n_{1}. \lambda n_{2}. \lambda n_3. n_{1}n_{2}n_{3}) c_{1}c_{2}c_{3} \end{eqnarray*}\]where $c_{1}=\textit{lang}$, $c_{2} \in \{ \texttt{slots}, \varnothing \}$ and $c_{3}=\textit{slug}$, we need to resolve context $c_{1}$ and $c_{3}$ through the resolvers $r(c_{1})$ and $r(c_{3})$ to obtain the bound values for types $\mathcal{C}_{lang}$ and $\mathcal{C}_{slug}$ respectively. Using the CMS one can implemented $r(c_{1})$ by retrieving the set of all supported languages and $r(c_{3})$ by enumerating all games supported by the system. For our example we will assume that the set $\mathcal{C}_{lang}$ and $\mathcal{C}_{slug}$ are
\[\begin{eqnarray*} &\mathcal{C}_{lang} = r(\textit{lang}) = \{ \texttt{en}, \texttt{fi}, \varnothing \}\\ &\mathcal{C}_{slug} = r(\textit{slug}) = \{ \texttt{gonzo}, \texttt{starburst}, \varnothing \} \end{eqnarray*}\]Substituting $\textit{lang}$ and $\textit{slug}$ with the set of bound variables $\mathcal{C}_{lang}$ and $\mathcal{C}_{slug}$
\[\begin{eqnarray*} &(\lambda n_1.\lambda n_2.\lambda n_3\cdot n_1n_2n_3)c_1 c_2 c_3\\ &\textrm{where}\\ &c_1 \in \{ \texttt{en, fi, }\varnothing \}\\ &c_2 \in \{ \texttt{slots, }\varnothing \}\\ &c_3 \in \{ \texttt{gonzo, starburst, }\varnothing \}\\ \end{eqnarray*}\]results in the bound expression set $\mathcal{RS}$.

We omitted $\varnothing$ for simplicity but there exist expression tree including $\varnothing$ in the expression set $\mathcal{RS}$ namely:
\[\begin{eqnarray*} &\psi(\omega(\varnothing\ \varnothing\ \varnothing)) \\ &\psi(\omega(\texttt{en}\ \varnothing\ \varnothing)) \\ &\psi(\omega(\texttt{fi}\ \varnothing\ \varnothing)) \\ &\psi(\omega(\texttt{en}\ \texttt{slots}\ \varnothing)) \\ &\psi(\omega(\texttt{fi}\ \texttt{slots}\ \varnothing)) \end{eqnarray*}\]99 Problems! Sitemap and Alternates ain’t one!
Having constructed the bound expression set we will now tackle the problem of serialising the complete sitemap and the problem of finding a list of alternate URLs from any given URL.
Getting all the paths of the site for sitemap
Having constructed the bound expression set we can obtain the set of URLs by passing each normalised expression through an internationalisation serialisation function $f_{int}$. For visualisation purposes, we shall display the serialised form after passing it through the serialisation function handling internationalisation $f_{int}$ below the node. Due to space limitations, we shall omit drawing the $\varnothing$ nodes.
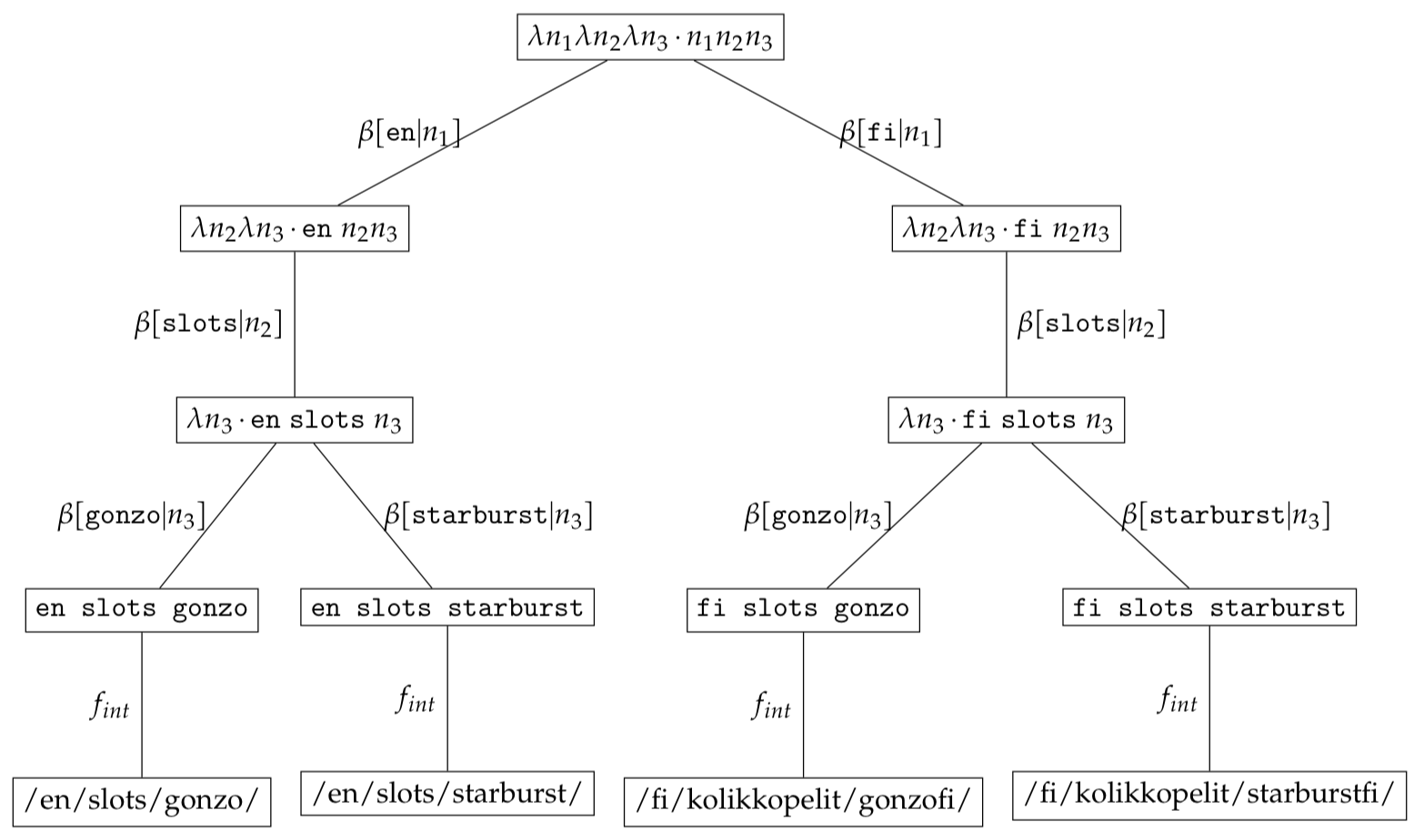
Since some paths might not be desired in the final list of URLs (sitemap) we will filter some deserialised URLs by passing them through a predicate $p$. Such a predicate needs to be based on the value of the variable $c_{k}$ present in the context. As an example the predicate $p(c) \rightarrow c_{1} \ne \texttt{en}$ will filter the serialised set
\[\begin{eqnarray*} &\{ \texttt{/en/slots/gonzo/}, \\ & \texttt{/en/slots/starburst/}, \\ & \texttt{/fi/kolikkopelit/gonzofi/}, \\ & \texttt{/fi/kolikkopelit/starburstfi/} \} \end{eqnarray*}\]As an implementation detail the CMS should include a flag on each sitemap and game element to indicate whether such an element is to be included in the sitemap. Such a flag needs to be encoded in a variable $c_{k}$ within the context.
to
\[\begin{eqnarray*} &\{\texttt{/fi/kolikkopelit/gonzofi/}, \\ & \texttt{/fi/kolikkopelit/starburstfi/} \} \end{eqnarray*}\]Getting alternate paths
Given a bound expression set $\mathcal{RS}$ how does one find all alternate URLs from a source URL? This problem can be solved by using the search functionality discussed in Section search . In essence we want to search the bound expression set $\mathcal{RS}$ using the normalised expression tree deserialised from the source URL. Since the language is not important the context $c_{1}$ - representing the language - will be marginalised in the search expression tree.
As an example, let us assume that a client requested the page /fi/kolikkopelit/gonzofi/ annotated with $^\dagger$ below.
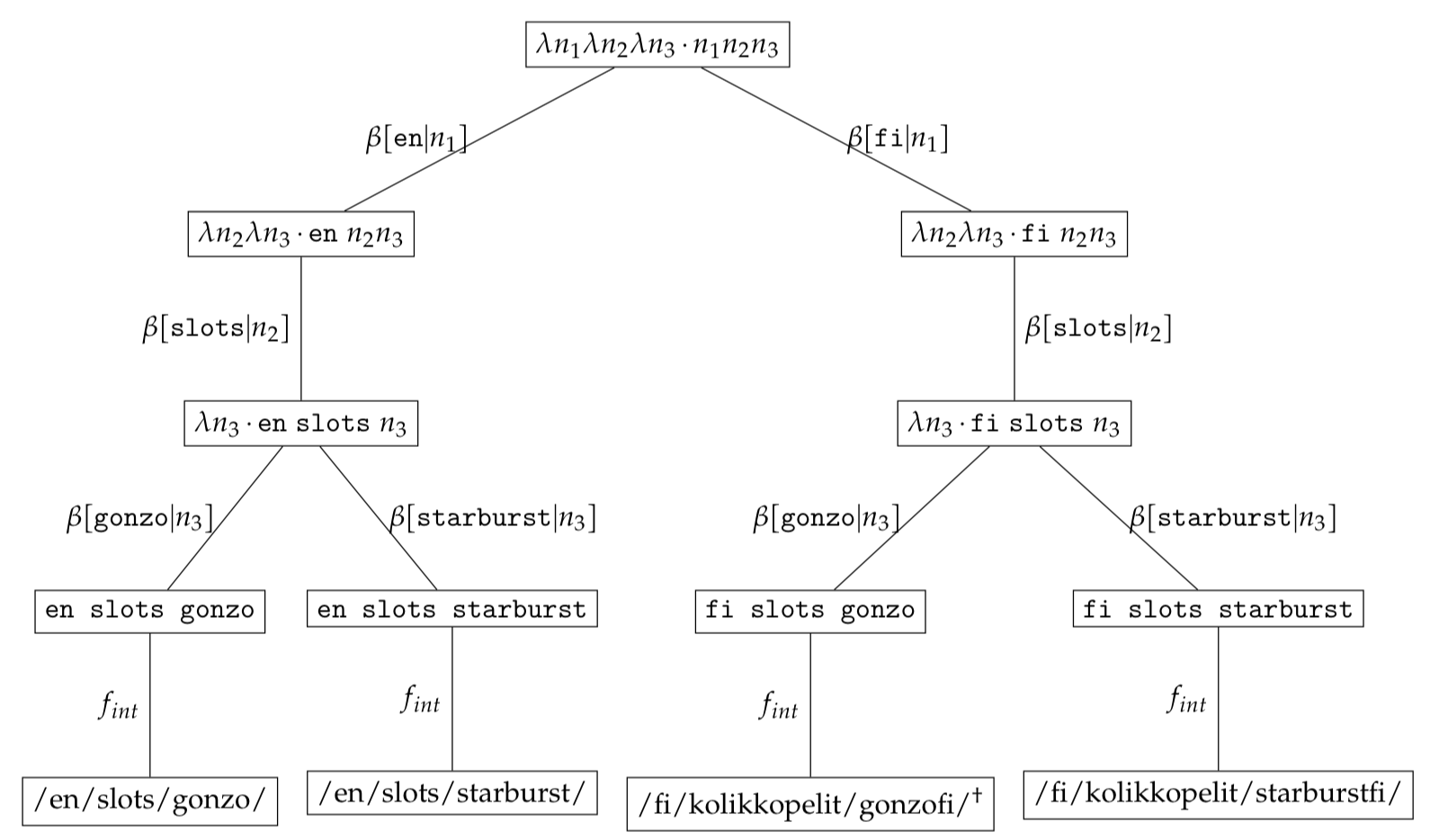
We can find the original normalised expression which serialised to $\texttt{/fi/kolikkopelit/gonzofi/}$ by using the inverse function $\bar{f_{int}}$
\[\begin{equation*} \bar{f_{int}}(/fi/kolikkopelit/gonzofi/) = \texttt{fi slots gonzo} \end{equation*}\]We convert the normalised expression $\texttt{fi slots gonzo}$ to the expression tree - $\psi(\omega(\texttt{fi slots gonzo}))$ - by using the $\omega$ function and work through the $\beta$-reductions. To search for similar expression trees which vary only in language we marginalise the language context by introducing a $\textit{free}$ variable $\ast$. We can obtain the set of alternate expression trees by applying
\[\begin{eqnarray*} \mathcal{RS}_{alternates}&=&search(\mathcal{RS}, \psi(\omega(\ast\ \texttt{slots gonzo}))\\ &=&\{\psi(\omega(\texttt{fi slots gonzo})), \psi(\omega(\texttt{en slots gonzo}))\} \end{eqnarray*}\]The expression set $\mathcal{RS}_{alternates}$ is then serialised using $f_{int}$ to obtain the set of alternate URLs
\[\begin{eqnarray*} f_{int}(\texttt{en slots gonzo})&=&\texttt{/en/slots/gonzo/}\\ f_{int}(\texttt{fi slots gonzo})&=&\texttt{/fi/kolikkopelit/gonzofi/} \end{eqnarray*}\]We will use the filter function $p(c) \rightarrow c_{1}\ne \texttt{en} \wedge c_{2} \ne \texttt{slots} \wedge c_{3} \ne \texttt{gonzo} $ to filter out the original URL.
Conclusion
In this post we have defined a model using $\lambda$-calculus which can be applied to common SEO problems namely the problem of retrieving all site URLs and the problem of retrieving all alternate URLs. Hopefully you find these ideas interesting! Stay safe and keep hacking!